ꕥ
3주차에도 이론에 많이 집중했습니다!
알고리즘 또한 이론을 알아야 이해하는데 수월하더라구요.
담주부터는 C언어합니다~
ꕥ
- LCS (Longest Common Subsequence)
- 최장 공통 부분 수열(LCS) : 두 개의 시퀀스(일련의 데이터)에서 가장 긴 부분 수열을 찾는 알고리즘
- 부분 수열 : 원래 수열에서 일부 요소를 선택하여 만든 수열이며, 선택된 요소들이 원래 수열에서 가진 순서를 유지

Ex) "ABCBDB"와 "BACDBC"의 최장 공통 부분 수열은 "ABC"이다. 이는 두 수열 모두에 속하며, 각 수열에서의 순서도 동일하게 유지되는 가장 긴 부분 수열이기 때문
- 활용 분야 : 두 시퀀스 간의 유사성을 찾아내는 것이 중요한 DNA, RNA 시퀀스 비교, 파일 비교 및 병합, 소프트웨어 버전 관리 등
- LCS 구현법 : 대표적으로 동적 프로그래밍(DP) 방법 사용
- LCS 계산 : 두 시퀀스의 일부분에 대한 LCS를 먼저 계산하고, 이를 활용하여 전체 시퀀스에 대한 LCS를 찾아내는 방식
- 동적 프로그래밍 : 큰 문제를 작은 문제로 나누어 풀고, 작은 문제의 결과를 이용하여 큰 문제를 해결하는 방법론

- 구현 단계
1. 테이블 초기화 : N*M 크기의 2차원 테이블을 생성하고, 모든 값을 0으로 초기화합니다. 여기서 N은 (첫 번째 Array1의 길이 + 1), M은 (두 번째 Array2의 길이 + 1)입니다. +1은 0행과 0열을 추가하기 위함입니다.
1) 경계 조건 처리 : 0행과 0열은 DP 테이블의 경계 조건을 처리하는데 도움을 줍니다. DP 테이블의 각 칸은 작은 문제의 해결 결과를 저장하는 공간인데, 각 칸의 값을 계산할 때 주로 왼쪽, 위, 왼쪽 위 칸의 값을 이용합니다. 만약 0행과 0열이 없다면, 테이블의 가장자리 칸에서 이러한 참조가 불가능하게 되어 별도의 경계 조건 처리가 필요하게 됩니다. 하지만 0행과 0열을 추가함으로써 모든 칸에서 일관된 방식으로 값을 계산할 수 있게 됩니다.
2) 빈 시퀀스 고려 : 0행과 0열은 2개의 Array 중 하나가 비어있는 경우를 고려한 것입니다. 만약 2개의 Array 중 하나가 비어있다면, 그들의 최장 공통 부분 수열은 당연히 비어있게 됩니다. 이 경우를 표현하기 위해 0행과 0열을 모두 0으로 채웁니다.
2. 테이블 채우기 : 순서대로 각 칸을 채워갑니다. i행 j열의 칸을 채울 때, 2개의 i-1번째 요소와 j-1번째 요소를 비교합니다. (두 Array의 인덱스는 0부터 시작합니다.)
1) 2개의 요소가 같다면, 왼쪽 위 칸(i - 1행, j - 1열)의 값에서 1을 더한 값을 해당 칸에 저장합니다.
2) 2개의 요소가 다르면, 왼쪽 칸(i행, j - 1열)과 위 칸(i - 1행, j열) 중에서 큰 값을 해당 칸에 저장합니다.
3. 최장 공통 부분 수열 찾기 : 테이블을 완성한 후, 마지막 칸의 값이 2개의 Array의 최장 공통 부분 수열의 길이를 나타냅니다. 마지막 칸에서 시작해서 왼쪽 위로 이동하면서 거꾸로 따라갑니다. 값이 바뀌는 위치를 찾으면, 그 위치에 해당하는 요소가 최장 공통 부분 수열에 속하는 것을 알 수 있습니다.
- 구현 코드
def LCS(arr1, arr2):
# DP 테이블 초기화
# 0행과 0열 또한 경계 조건 처리
dp = [[0] * (len(arr2) + 1) for a in range(len(arr1) + 1)]
print(dp)
# DP 테이블 채우기
for i in range(1, len(arr1) + 1):
for j in range(1, len(arr2) + 1):
# arr1과 arr2의 값이 같다면
if arr1[i-1] == arr2[j-1]:
# 좌측 대각선 값을 +1 후 기입
dp[i][j] = dp[i-1][j-1] + 1
# 값이 같지 않다면
else:
# 값이 다른 위치의 위와 왼쪽 중 최대값을 기입
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
# 최장 공통 부분 수열 찾기
i, j = len(arr1), len(arr2)
lcs = []
# 마지막 칸에서 시작해서 왼쪽 위로 이동하면서 거꾸로 확인
while i > 0 and j > 0:
# arr1과 arr2의 값이 같다면
if arr1[i-1] == arr2[j-1]:
lcs.append(arr1[i-1])
i -= 1
j -= 1
# 현재 위치의 위쪽 값이 왼쪽 값보다 크다면
# 위쪽 값이 더 긴 공통 부분 수열을 가지므로 위쪽으로 이동
elif dp[i-1][j] > dp[i][j-1]:
i -= 1
# 현재 위치의 왼쪽 값이 위쪽 값보다 크거나 같다면
# 왼쪽으로 이동
else:
j -= 1
# LCS를 원래 순서대로 뒤집기
lcs.reverse()
return lcs
# 예제 실행
arr1 = ['A', 'B', 'C', 'B', 'D', 'B']
arr2 = ['B', 'A', 'C', 'D', 'B', 'C']
# arr1 = ['A', 'C', 'A', 'Y', 'K', 'P']
# arr2 = ['C', 'A', 'P', 'C', 'A', 'K']
print(LCS(arr1, arr2)) # ['B', 'C', 'D', 'B']
# print(LCS(arr1, arr2)) # ['A', 'C', 'A', 'K']- 배열의 할당과 접근
- C의 배열 : 스칼라 데이터를 보다 큰 자료형으로 연계 시키는 수단이며, Pointer 기반으로 한 구조
- 스칼라 데이터 : 1개 값만을 저장할 수 있는 자료형
Ex) Integer
- 컴포지트 데이터 : 2개 이상의 복합적인 값을 저장할 수 있는 자료형
Ex) Enumerations
- C가 기계어 번역이 쉬운 이유
- 저수준 언어 : C언어는 저수준 언어 특성을 가지고 있어, 하드웨어를 직접 제어하는 것이 가능합니다. 메모리 접근, 비트 단위 연산 등이 가능하며, 이런 특성들은 기계어로 번역하기 상대적으로 단순하게 만듭니다.
- 명령어 집합과의 유사성 : C언어의 구문과 구조는 프로세서의 명령어 집합과 매우 유사합니다. 따라서 C언어로 작성된 코드를 기계어로 번역하는 것이 상대적으로 간단합니다.
- 컴파일러의 최적화 : C언어의 컴파일러는 코드를 효율적인 기계어로 변환하는데 있어 매우 효과적입니다. 최적화 단계에서 컴파일러는 불필요한 코드를 제거하고, 반복문을 풀어내며, 메모리 접근을 효율화 하는 등 다양한 최적화 기법을 적용합니다.
- C의 다중 배열 : 배열의 원소들은 메모리에 ‘행 우선’ 순서로 저장
- 배열 표현법
- E[i] : E의 주소 : %rdx, i : %rcx
- 주소 계산 : Xe + 4i
- 결과 레지스터 : %eax
- 표현 : movl(%rdx, %rcx, 4), %eax
- 표 1
- Data Size, Index
char A[12];
char *B[8];
int C[6];
double *D[5];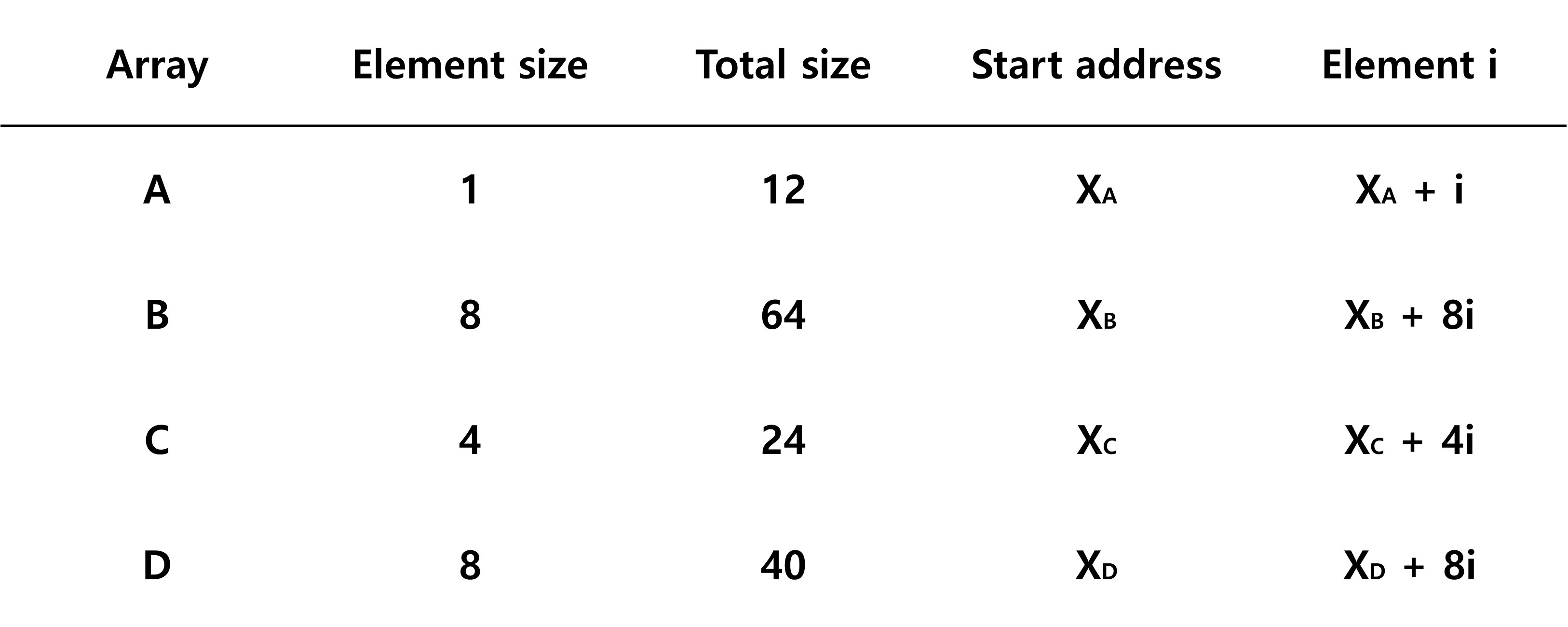
- 표 2
- Data Size, Index
- Hint : 모든 종류의 Pointer은 8Byte, Int 4Byte, Short 2Byte
int P[5];
short Q[2];
int **R[9];
double *S[10];
short *T[2];
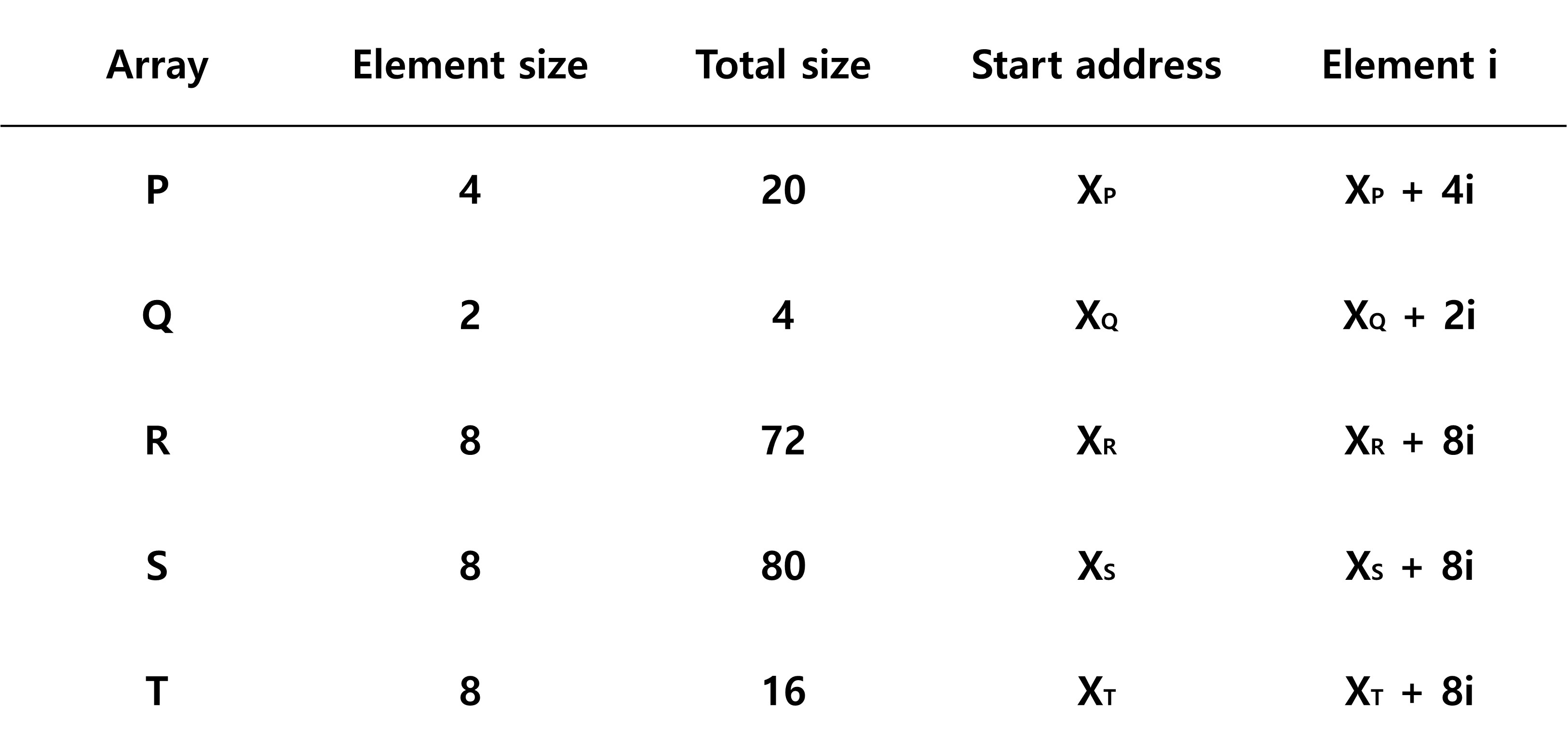
- Pointer
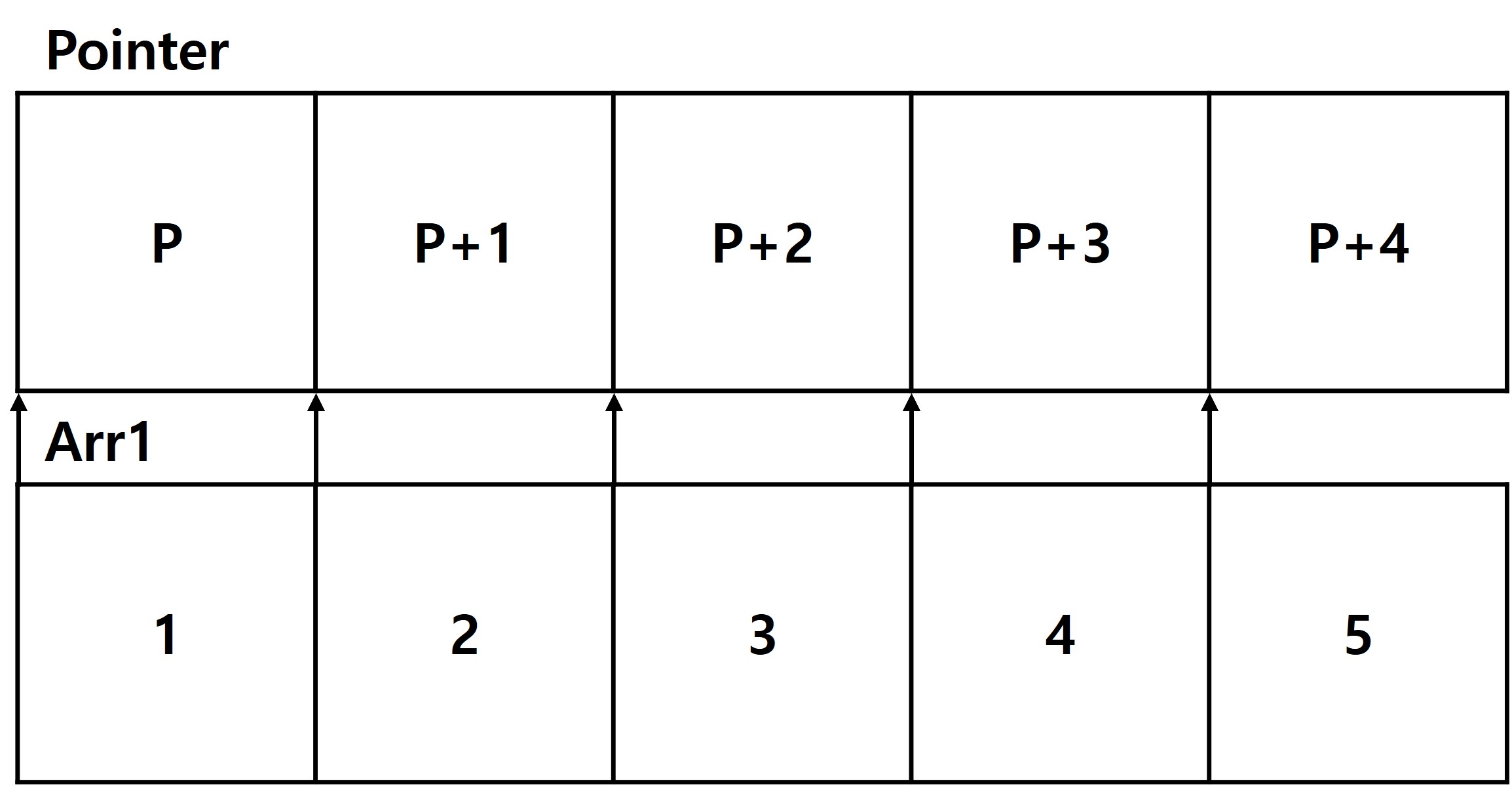
- Pointer 선언 시 반드시 포인터가 가리킬 자료형을 명시
- 선언한 Pointer 자료형의 크기에 따라 주소값의 증가폭이 다름
int *pInt;
char *pChar;
float *pFloat;- 배열의 이름은 배열의 시작 주소이며, 배열의 첫번째 주소를 가지는 Pointer와 동일
- 객체 Expr가 있을 때, 객체의 주소는 &Expr
- '&' 연산자를 이용해서 변수의 주소를 얻어 해당 Pointer에 할당
- 주소를 나타내는 AExpr 변수에 대해, 그 주소의 위치한 값 *AExpr
- '*' 연산자를 이용하여 Pointer를 역참조해서 실제 메모리 주소에 저장된 값에 접근
- Expr와 *&Expr는 동일
- 배열 참조 Arr1[i]와 *(Arr1+i) 동일
- A+i는 배열의 시작 주소에서 i만큼 떨어진 주소
- Aassembly : 컴퓨터의 기계어에 대한 저수준 Programming Language

- 고정 크기 배열
- 최적화 방안 : 프로그램에서 배열의 차원이나 버퍼의 크기 설정 시, 매번 숫자를 사용하는 것보다 #define을 선언해 일괄적으로 변수를 관리하는 것이 용이
# define N 16
typedef int fix_matrix[N][N];- 가변 크기 배열
- 배열이 할당될 때 배열의 차원을 계산할 수 있는 방안 : 배열을 지역 변수나 함수의 인자로 선언
int var_ele(long n, int A[n][n], long i, long j) {
return A[i][j];
}- 함수 전달 원리
- Call by value : 원본 값에 변화 없음
int swap(int x, int y) {
int temp;
temp = x;
x = y;
y = temp;
}
int main() {
int a = 3, b = 5;
swap(a, b);
printf("%d %d", a, b);
return 0;
}- Call by address : 원본 값을 변화 시킴
int swap(int *p1, int *p2) {
int temp;
temp = *p1;
*p1 = *p2;
*p2 = temp;
}
int main() {
int a = 3, b = 5;
swap(&a, &b);
printf("%d %d", a, b);
return 0;
}'Krafton Jungle' 카테고리의 다른 글
| [ KJ ] Week06 (0) | 2024.02.29 |
|---|---|
| [ KJ ] Week05 (1) | 2024.02.23 |
| [ KJ ] Week04 (0) | 2024.02.07 |
| [ KJ ] Week02 (1) | 2024.01.26 |
| [ KJ ] Week01 (0) | 2024.01.18 |
![[ KJ ] Week03](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FckH7F0%2FbtsEjHUFUp6%2FPTIlHOPs3TKdkuvQXDoYi0%2Fimg.jpg)